SI100B EE Part · Tutorial 2

Exercise 1: Multiplier

在上一次作业里，我们已经实现了加法和减法。现在我们要尝试一些更复杂的运算：乘法。

什么，你问时序逻辑去哪里了？娄老师说他不讲了！

在硬件电路中，乘法有很多种实现方式：我们可以通过不断进行移位的乘法和加法来实现，也可以通过引入更多的硬件资源，在一个组合电路中直接实现乘法运算。

在本次 Exercise 里，我们实现一个比较简单的版本：

• 直接通过模拟乘法的运行规律来实现一个“四位+四位->八位”的乘法器！

Exercise 1: Multiplier

1.1. 引入：十进制乘法运算过程

我们首先分析在十进制下，我们通过列竖式计算，将两个数字相乘时的计算思路：

• 我们将两数中的被乘数完整保留，与被逐位拆分的乘数分别进行乘法运算，从而获得“部分积”
• 然后，我们再为每个部分积追加位权（这也就是为什么竖式要求将部分积错位相加）
• 最终，我们把相加得到乘积。

Exercise 1: Multiplier

1.1. 引入：十进制乘法运算过程

依照常识，我们约定：

1. 被乘数指四则运算的乘法中被乘的数字，一般来说放在算式的前面。
   • 如：4×2=8: 上述算式中，4是被乘数，2是乘数
2. 在乘法中，如果乘数是两位或两位以上的数，乘的时候，就要用乘数的每一位去乘被乘数，每次乘得的积，叫做部分积，或叫做不完全积。
3. 位权指数码在不同位置上的权值。在进位计数制中，处于不同数位的数码代表的数值不同：如十进制数111，个位数上的1 的权值为 ，十位数上的1 的权值为 ，百位数上的1 的权值为 。

Exercise 1: Multiplier

1.1. 引入：十进制乘法运算过程

例如，三位数 abc 与 xyz 相乘（每一个字母代表相应数位上的数字）：

abc * xyz = x * abc * 100 + y * abc * 10 + z * abc * 1

Exercise 1: Multiplier

1.2. 二进制乘法运算过程

在数字系统中，乘法运算是以二进制的形式进行的，不妨研究一位二进制数相乘的情况：

000 * 000 = 000;
000 * 001 = 000;

001 * 000 = 000;
001 * 001 = 001;

不难看出，一位二进制数相乘，实质上是进行逻辑与运算。

Exercise 1: Multiplier

1.2. 二进制乘法运算过程

接下来考虑两位二进制数与一位二进制数相乘：

010 * 000 = 000;
010 * 001 = 010;

011 * 000 = 000;
011 * 001 = 011;

也不难看出，以上运算事实上是一位二进制数对两位二进制数按位取逻辑与运算。

Exercise 1: Multiplier

1.2. 二进制乘法运算过程

接下来再考虑两位二进制数相乘：

010 * 010 = 100 = 10 * 1 * 10 + 10 * 0 * 1 = 100 + 0;

010 * 011 = 110 = 10 * 1 * 10 + 10 * 1 * 1 = 100 + 10;

011 * 010 = 110 = 11 * 1 * 10 + 11 * 0 * 1 = 110 + 0;

011 * 011 = 1001 = 11 * 1 * 10 + 11 * 1 * 1 = 110 + 11;

Exercise 1: Multiplier

1.2. 二进制乘法运算过程

我们可以通过一个Python位运算的例子来理解移位操作。

Python中的二进制乘法可以通过位运算符实现。具体来说，就是使用 & 运算符进行按位与操作，使用 << 运算符进行左移操作。

例如，将二进制数1010左移两位，即可得到101000，相当于将原数乘以2的2次方。

我们尝试在 Python 中实现一个简单的二进制乘法函数，来理解乘法器的原理：

• a 和 b 分别表示要相乘的两个二进制数
• result 表示最终的乘积
• 在每次循环中，我们需要判断 b 的最低位是否为1
  • 如果是，我们将 a 加到 result 中；否则，我们什么也不做。
  • 然后，我们将 a 左移一位，b 右移一位，进入下一次循环，直到 b == 0。
• 你可以通过 print 函数来输出中间结果。

Exercise 1: Multiplier

1.2. 二进制乘法运算过程

def binary_multiply(a: int, b: int) -> int:
    result: int = 0
    while (b > 0):
        if (b & 1):
            result += a
        a <<= 1
        b >>= 1
    return result

Exercise 1: Multiplier

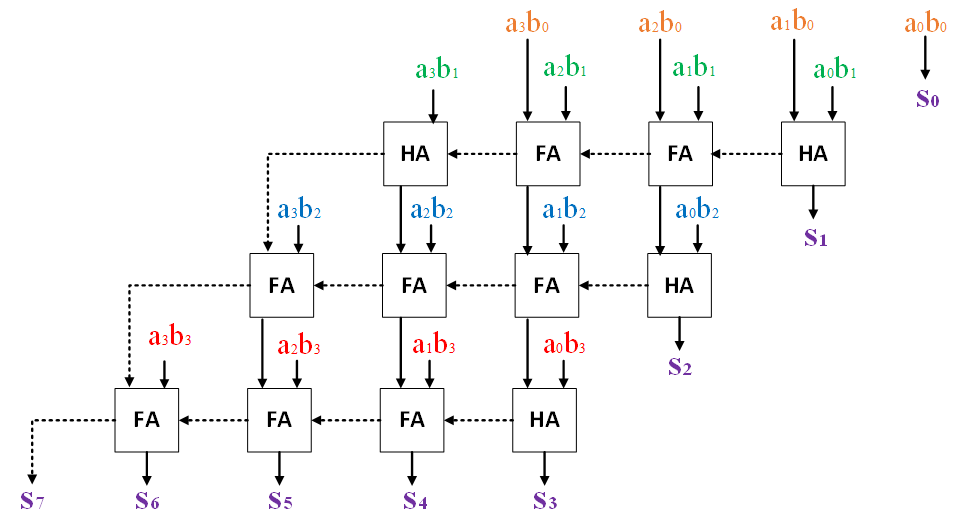
1.3. 阵列乘法器

阵列乘法器模拟了上述 Python 程序的二进制乘法运算过程：

• 将乘数逐位拆分，与被乘数的各个位进行逻辑与运算，得到一组二进制部分积。
• 部分积作为每一位的被加数输进加法器中，与下一级的部分积进行相加操作，加法器会输入上一位的进位，然后将本级进位输出到下一位的加法器中。
• 随着部分积的位权由低到高，通过逐级左移一位排布的加法器阵列，可以模拟乘法的过程，并且输出结果。

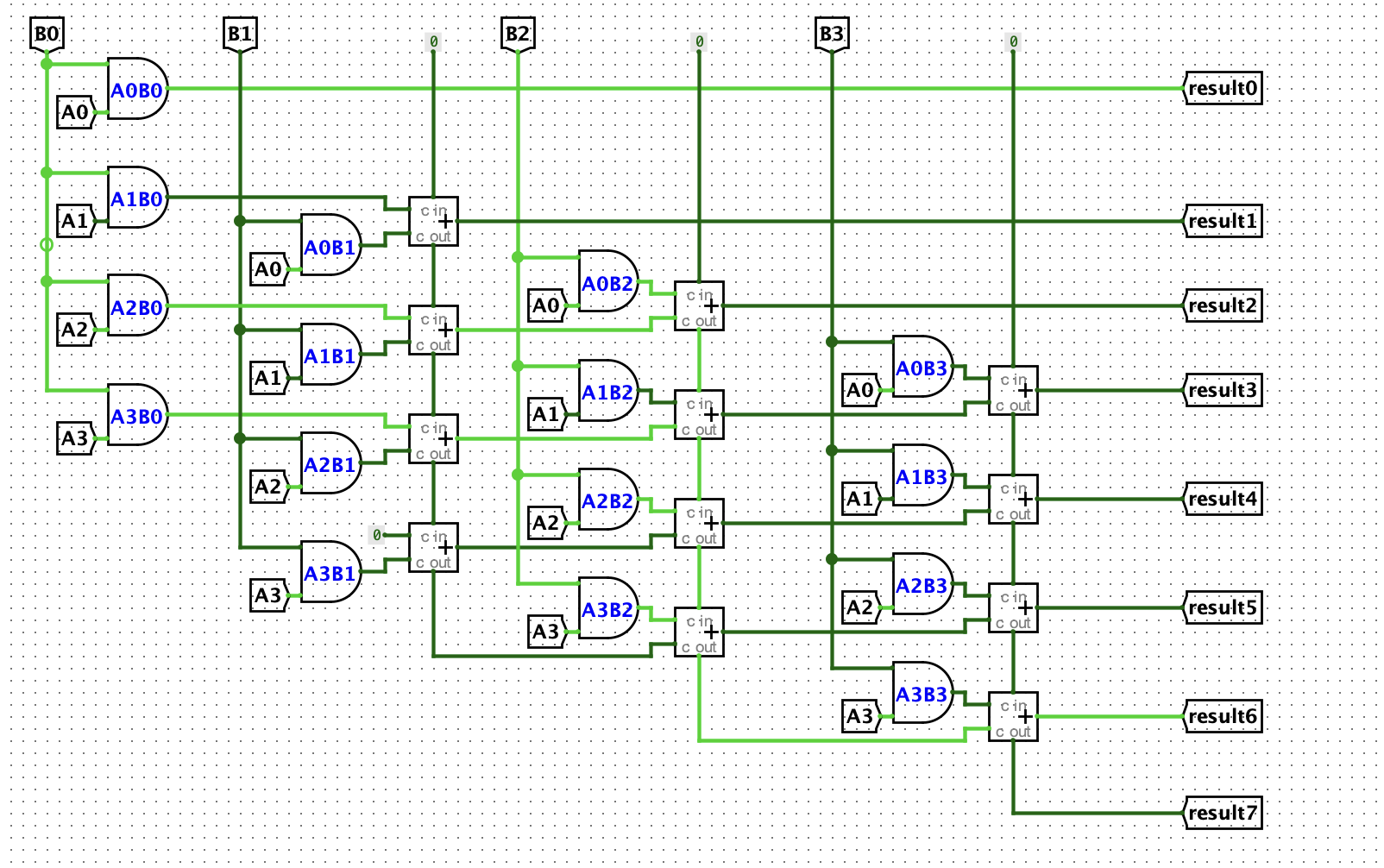
1.4. 输入、输出和实现要求

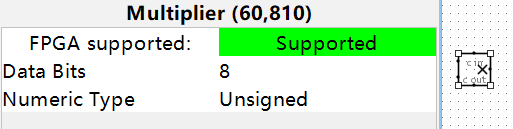
• 输入： 乘法器接受两个 4 位的二进制数 A 和 B。
• 输出： 乘法器输出一个 8 位的二进制数 result，表示 A 和 B 的乘积。
• 实现要求： 你需要使用 Logisim 实现这个乘法器，其中你可以使用 Logisim 自带的加法器实现加法和移位操作，但不允许使用 Logisim 自带的乘法器。

An Example of Multiplier

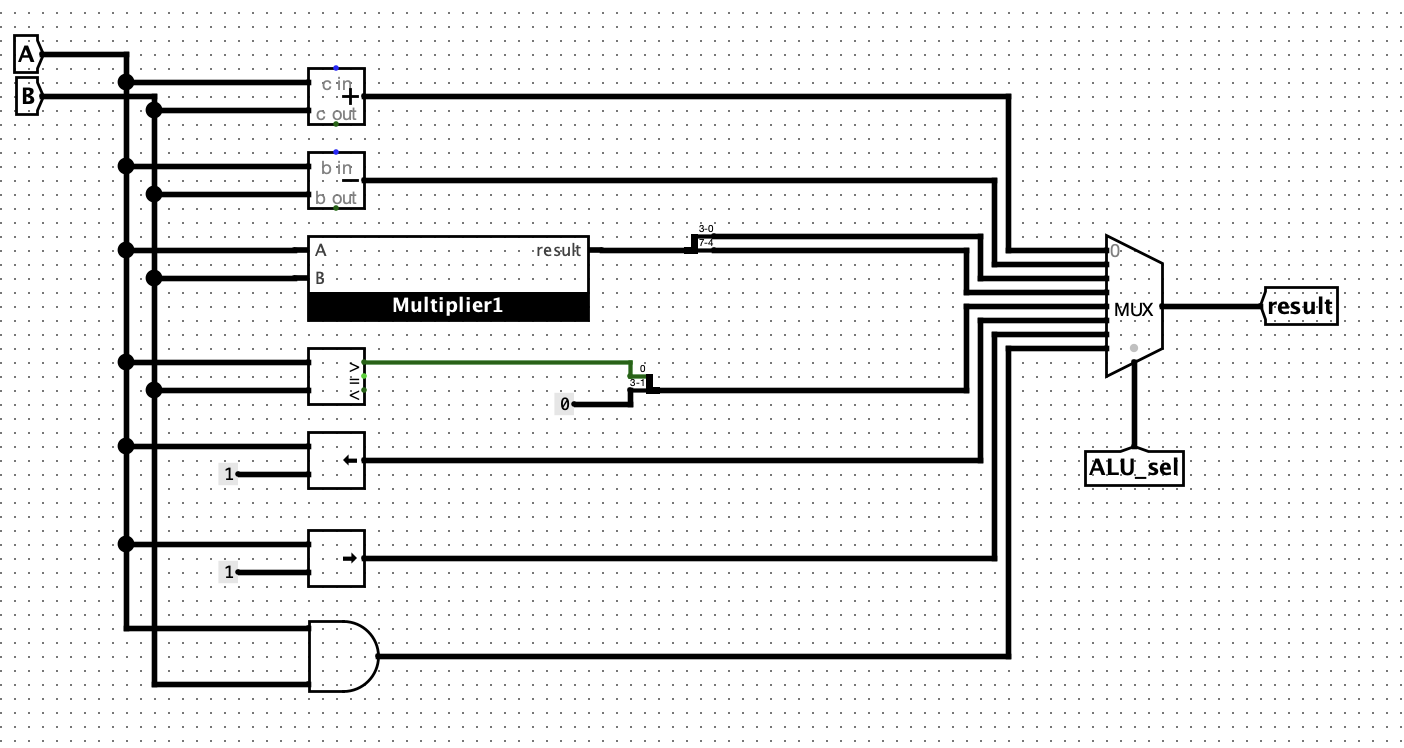
Exercise 2: 简易 ALU

在这个 Exercise 里，我们需要用结合之前所学的知识（选择器、加法器、减法器等），搭建一个 ALU。

• ALU 的乘法器部分需要使用你在 Exercise 1 中实现的乘法器，不允许使用 Logisim 自带的乘法器。

Exercise 2: 简易 ALU

2.1 ALU 介绍

ALU（Arithmetic & Logic Unit，算术逻辑单元）是计算机中进行所有数字计算和逻辑操作的核心部件。它根据选择信号执行不同的操作，包括算术运算、位逻辑运算和移位运算等。

在本题中，我们需要设计一个 共11 位输入的 ALU：

• 输入端：

  • 数据输入 A：一个 4 位数（A[3:0]）
  • 数据输入 B：一个 4 位数（B[3:0]）
  • 选择信号 ALU_sel：一个 3 位数，用于选择 8 种不同的操作（ALU_sel[2:0]）。

• 输出端：

  • 数据输出 result：一个 4 位数，根据选择信号的不同，ALU 执行以下 8 种操作：

通过设计这个 ALU，你将能够实现多种算术和逻辑操作，从而为计算机系统中的数据处理提供基础支持。

Exercise 2: 简易 ALU

2.3 ALU 操作细节说明

• 加法： 当 ALU_sel = 000 时，ALU 执行加法运算，result = A + B。
• 减法： 当 ALU_sel = 001 时，ALU 执行减法运算，result = A - B。
• 乘法： 当 ALU_sel = 010 时，ALU 输出乘法结果的低四位，即 (A * B)[3:0]；当 ALU_sel = 011 时，ALU 输出乘法结果的高四位，即 (A * B)[7:4]。
• 比较（A > B）： 当 ALU_sel = 100 时，ALU 比较 A 和 B 的大小。如果 A 大于 B，输出 1，否则输出 0。
  • 我们的比较操作是无符号比较。在 Logisim 中，需要通过修改内置比较器的默认设置来实现无符号比较。
  • “无符号”的英文是 unsigned，而默认的操作是补码比较，其英文为 complement。
• 左移： 当 ALU_sel = 101 时，ALU 对 A 执行左移操作，result = A << 1。
• 右移： 当 ALU_sel = 110 时，ALU 对 A 执行右移操作，result = A >> 1。
• 按位与： 当 ALU_sel = 111 时，ALU 执行按位与操作，result = A & B。

Exercise 2: 简易 ALU

2.3 ALU 操作细节说明

以下是著名的74LS181计算逻辑单元：

Exercise 2: 简易 ALU

2.4 输入、输出和实现要求

• 输入： ALU 接受两个 4 位的数字 A 和 B，以及一个 3 位的选择信号 ALU_sel。
• 输出： ALU 输出一个 4 位的结果 result，它是根据选择信号 ALU_sel 所指定的运算结果。
• 实现要求： 你需要使用 Logisim 实现这个 ALU，其中乘法器部分需要使用你在 Exercise 1 中实现的乘法器；除此之外，你可以使用 Logisim 自带的加法器、减法器、比较器、移位器和 MUX 等组件。

An Example of ALU