1.1. 理解真值表
1.1.2. 理解真值表-以全加器为例
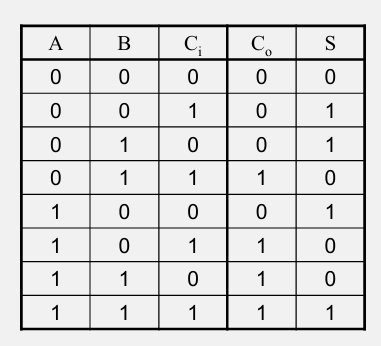
以一个三输入的全加器为例,全加器的作用是将两个 1 位(1-Bit)的二进制数相加,并考虑到可能的进位。
- 输入:设输入为A、B、C
- A 和 B 为加数
- Cin 为进位
- 输出:设输出为 S(和,Sum)和 Cout(新的进位)
关于 Full Adder 更详细的讲解,你可以在 Homework 1 的题目中看到!
1.2. SOP(Sum Of Product)
SOP形式是用“与”(Product,或者称 And)项(称为 Product Terms)的“相加”(Add,或者称 Or)来表达逻辑函数,这些 Product Term 中的每个都能导致逻辑函数输出为 1 。
1.2. SOP(Sum Of Product)
1.2.1. Standard SOP(最小项)
标准SOP形式中的每个product term都应该包含逻辑函数中的所有变量,无论是原始变量还是其反转形式。
例如,对于一个三输入函数
1.2. SOP(Sum Of Product)
1.2.2. 通过真值表得到 Standard SOP
仍以全加器为例,观察真值表中 Sum(
- 对于输出 S ,真值表中
- 对于输出 Cout(新的进位),
1.3. 布尔代数与逻辑函数化简
布尔代数提供了一系列规则,用于逻辑函数的化简,使之可以用更少的逻辑门电路实现相同的功能。
1.3.1.常见布尔代数规则

1.3. 布尔代数与逻辑函数化简
1.3.2 使用布尔代数化简SOP
虽然布尔代数可以用于化简逻辑函数,但是这种方法的局限性在于,可能无法找到逻辑函数的最简形式。尤其是对于包含多个变量的函数,手动化简可能既复杂又容易出错。
1.4. 利用卡诺图化简
卡诺图是真值表的图形化表示。一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各项最小项相应地填入一个特定的方格图内,此方格图为卡诺图。
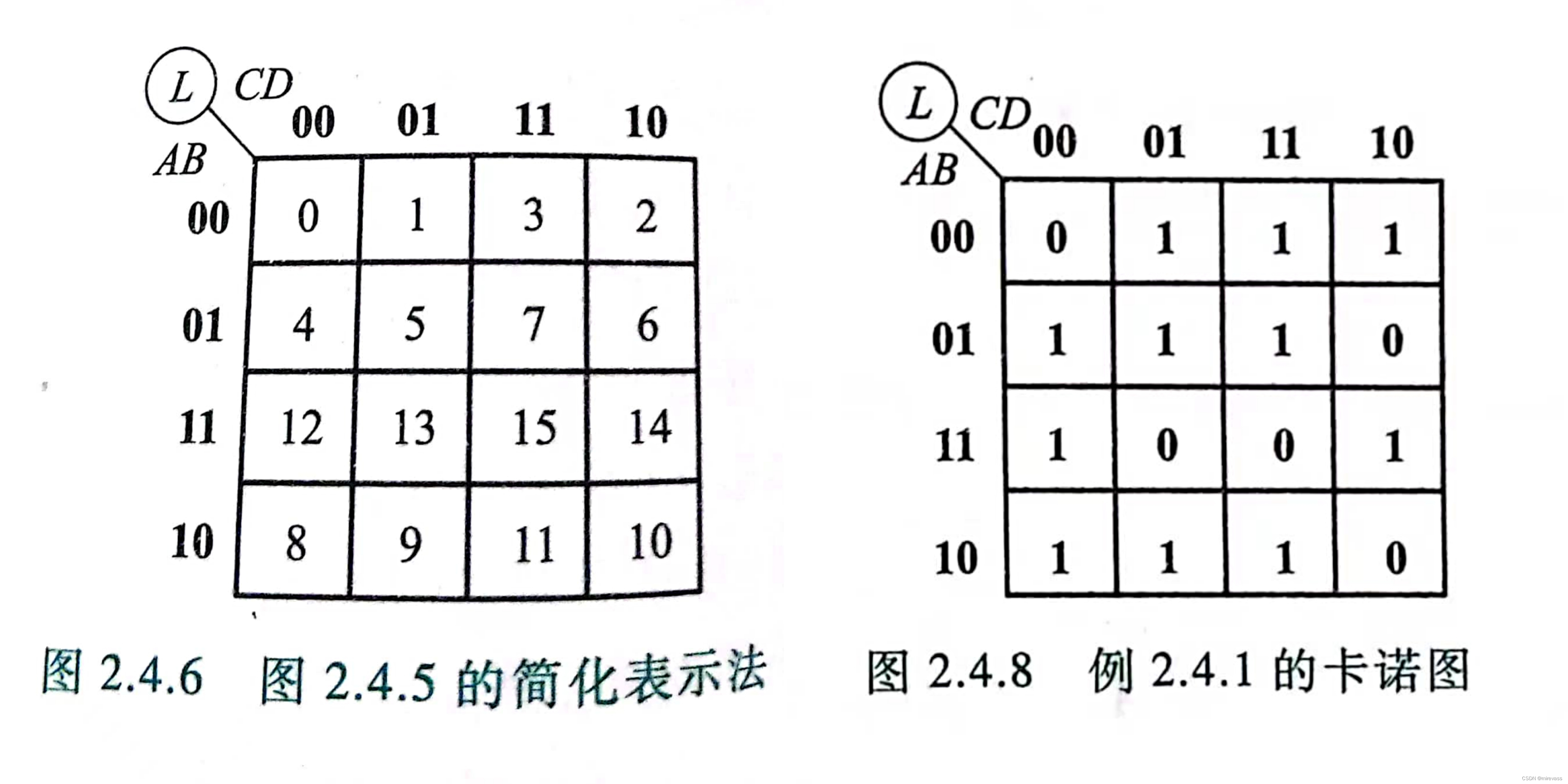
左图为最小项的序号排列,右图为表达式对应的最小项
1.4. 卡诺图
1.4.1. 利用卡诺图化简
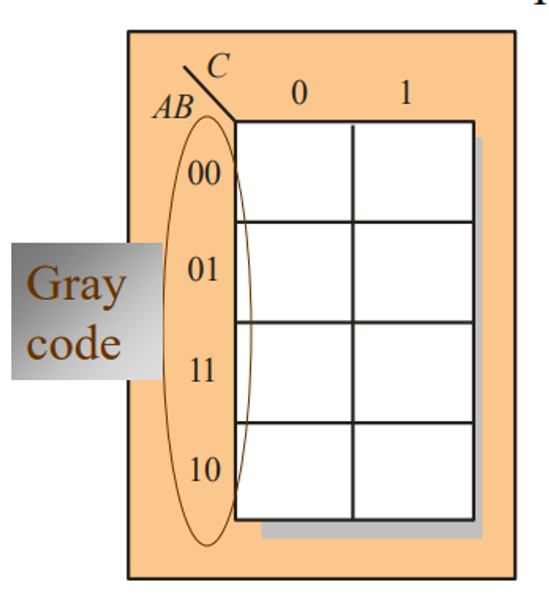
为什么两侧的数值不采用二进制数从小到大进行排列(事实上,这种排列形式叫“格雷码”)?
- 为了保证图中几何位置相邻的最小项在逻辑上也具有相邻性,两个相邻的最小项仅有一个变量是不同的。
局限性:只能化简小于等于四个变量,(五个变量也可以,但一般不用)
1.4. 卡诺图
1.4.2 卡诺图化简规则
- 卡诺图的边缘是相连的,即:最左边的列与最右边的列相邻,最上面的行与最下面的行相邻。
- 将所有输出为1的方格圈起来,每个圈应该包含
- 尽量使用大的圈来减少表达式中变量的数量。
- 确保卡诺图中的每个1至少被一个圈覆盖。
- 圈的数量应该尽可能少,这样可以确保最终的表达式尽可能简单。
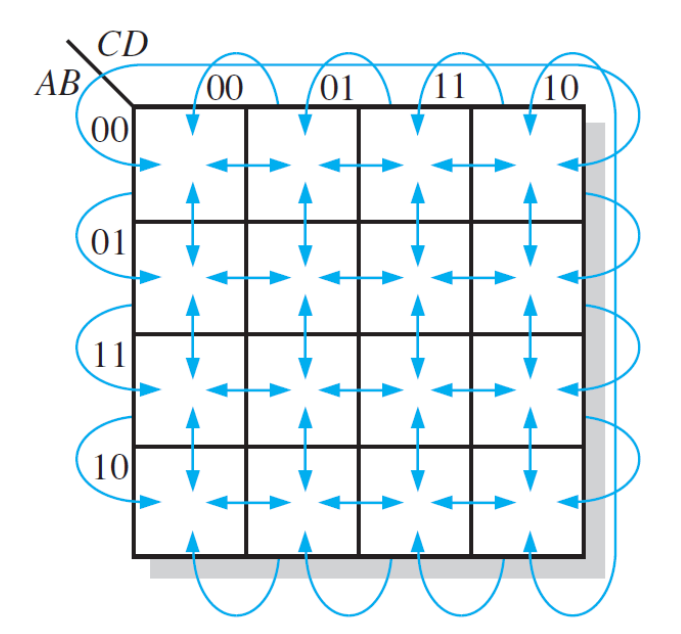
1.4. 卡诺图
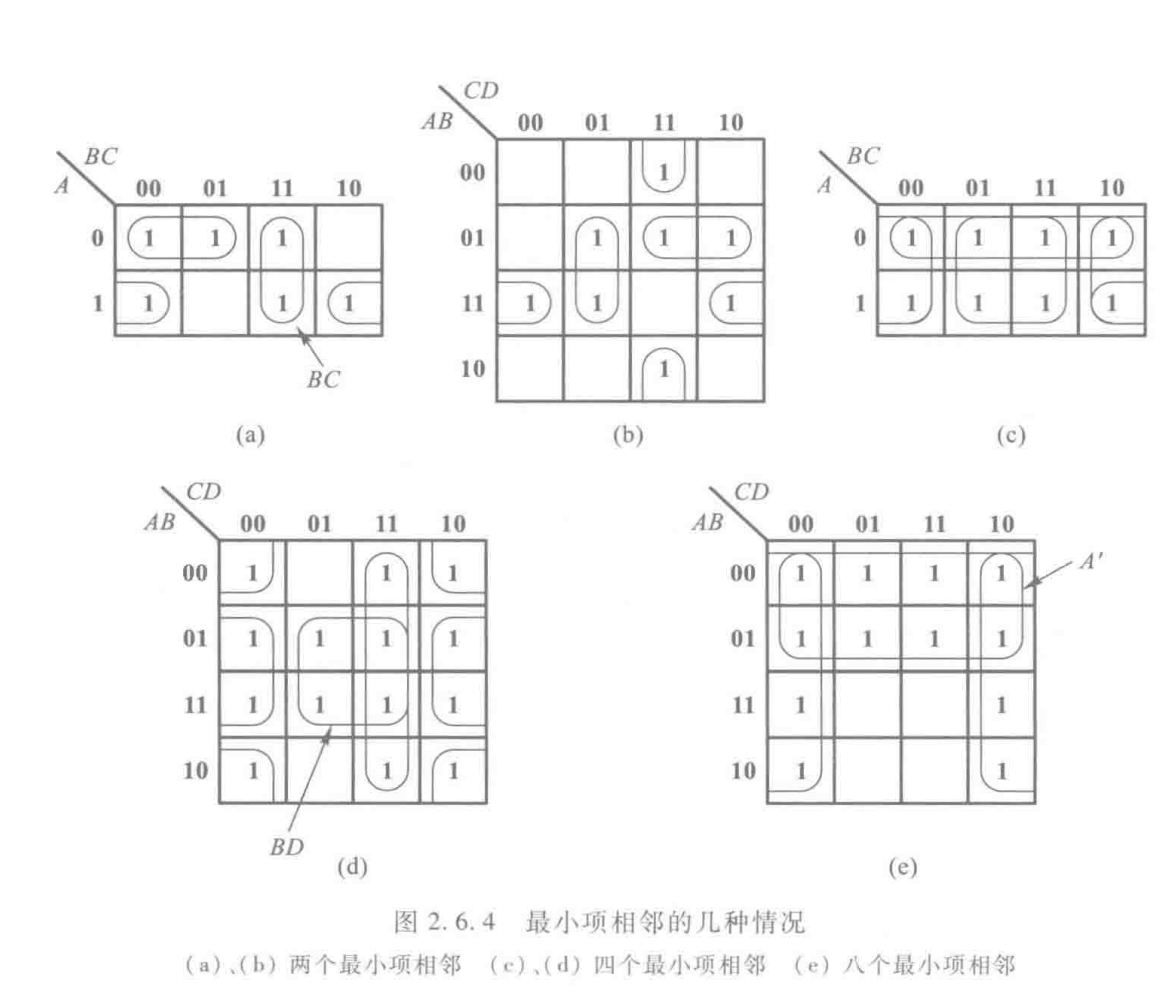
1.4.2 卡诺图化简规则:例子
这是一些不同大小的卡诺图。
- 我们要尽量把相邻的“1”合并
- 注意,跨过边缘的“1”们也是相邻的!
1.5. 绘制组合逻辑电路
基于化简后的逻辑表达式,可以选择合适的逻辑门来实现相应的逻辑功能。
- 与门(AND Gate)用于实现逻辑乘(AND)操作。
- 或门(OR Gate)用于实现逻辑加(OR)操作。
- 非门(NOT Gate)用于实现逻辑反转(NOT)操作。
例如,对于前述全加器中S的逻辑表达式
- 使用四个非门分别处理所有变量的反转。
- 使用与门处理每个 Product term。
- 最后使用或门将所有 Product terms 的结果合并输出。
1.6. 例子
根据上面所学到的步骤,尝试搭建一个红绿灯故障检测的电路:
使用逻辑门电路设计一个监视交通信号灯工作状态的逻辑电路。每一组信号灯均由红、黄、绿三盏灯组成,如下图所示。正常工作情况下,任何时刻必有一盏灯点亮,而且只允许有一盏灯点亮。而当出现其他五种点亮状态时,电路发生故障,这时要求发出故障信号,以提醒维护人员前去修理。
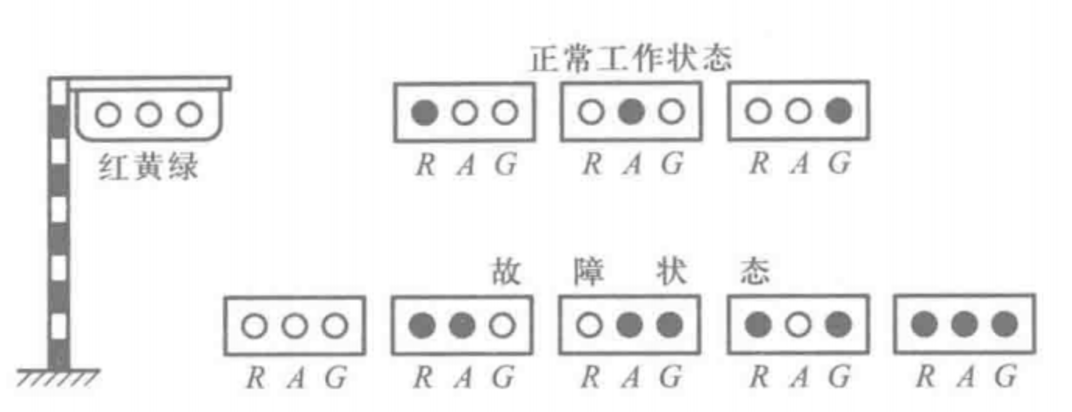
1.6. 例子
Step 0:进行逻辑抽象
取红、黄、绿三盏灯的状态为输入变量,分别用 R、A、G 表示,并规定灯亮时为 1,不亮时为 0。
取故障信号为输出变量,以 Z 表示之,并规定正常工作状态下 Z 为 0,发生故障时 Z 为 1。
1.6. 例子
Step 1:画真值表
| R | A | G | Z |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Step 2:最小项
找 Z=1 时对应的 R、A、G 的值
1.6. 例子
Step 3:利用卡诺图进行化简
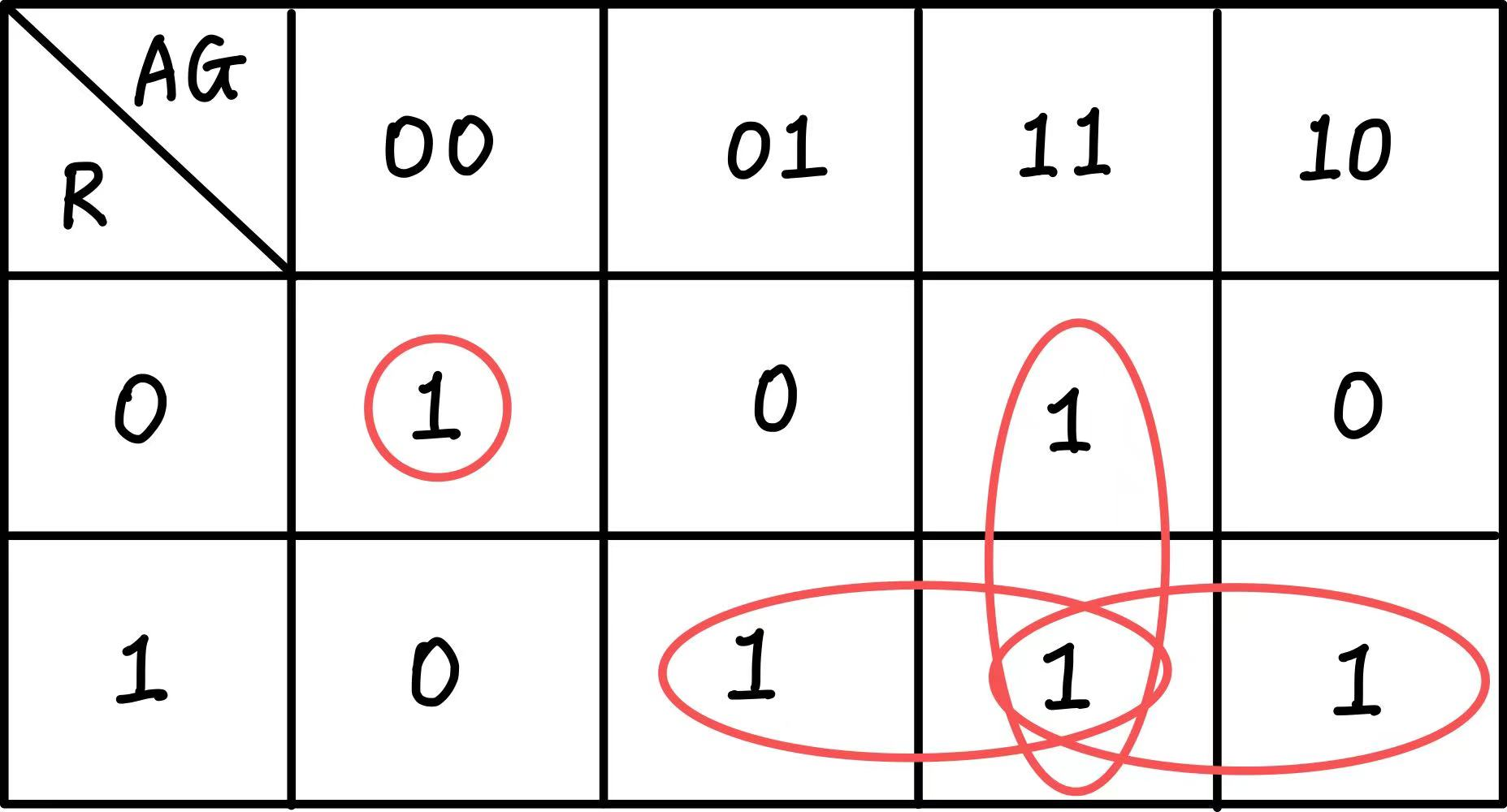
化简后的逻辑表达式为:
Step 4:画电路图
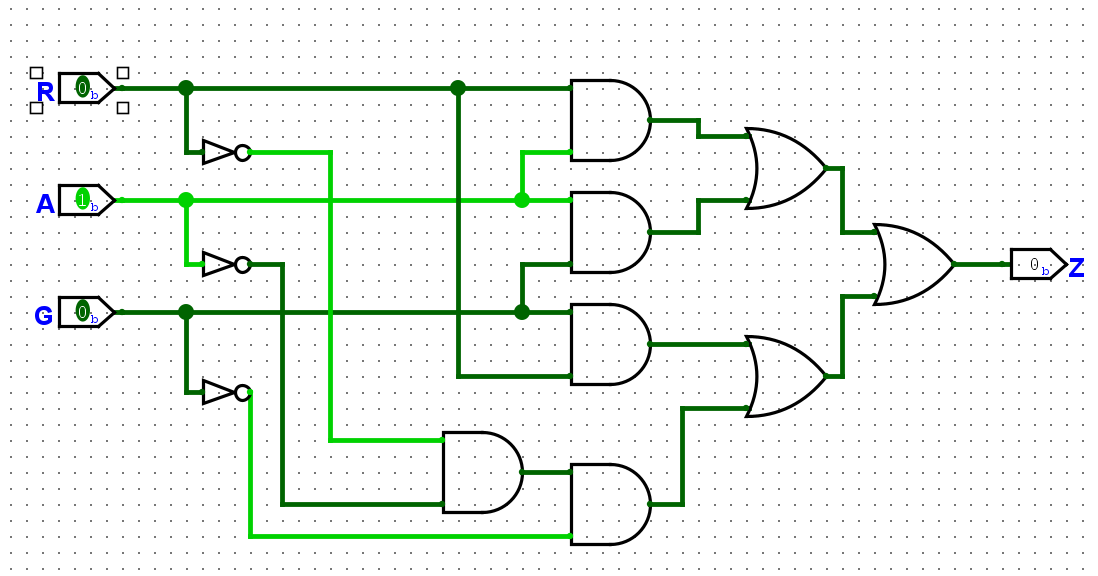
2. Practice Example
2. Practice Example
跟着我们一起来实践一下吧!
3. Homework 1 Guide
3. Homework 1 Guide
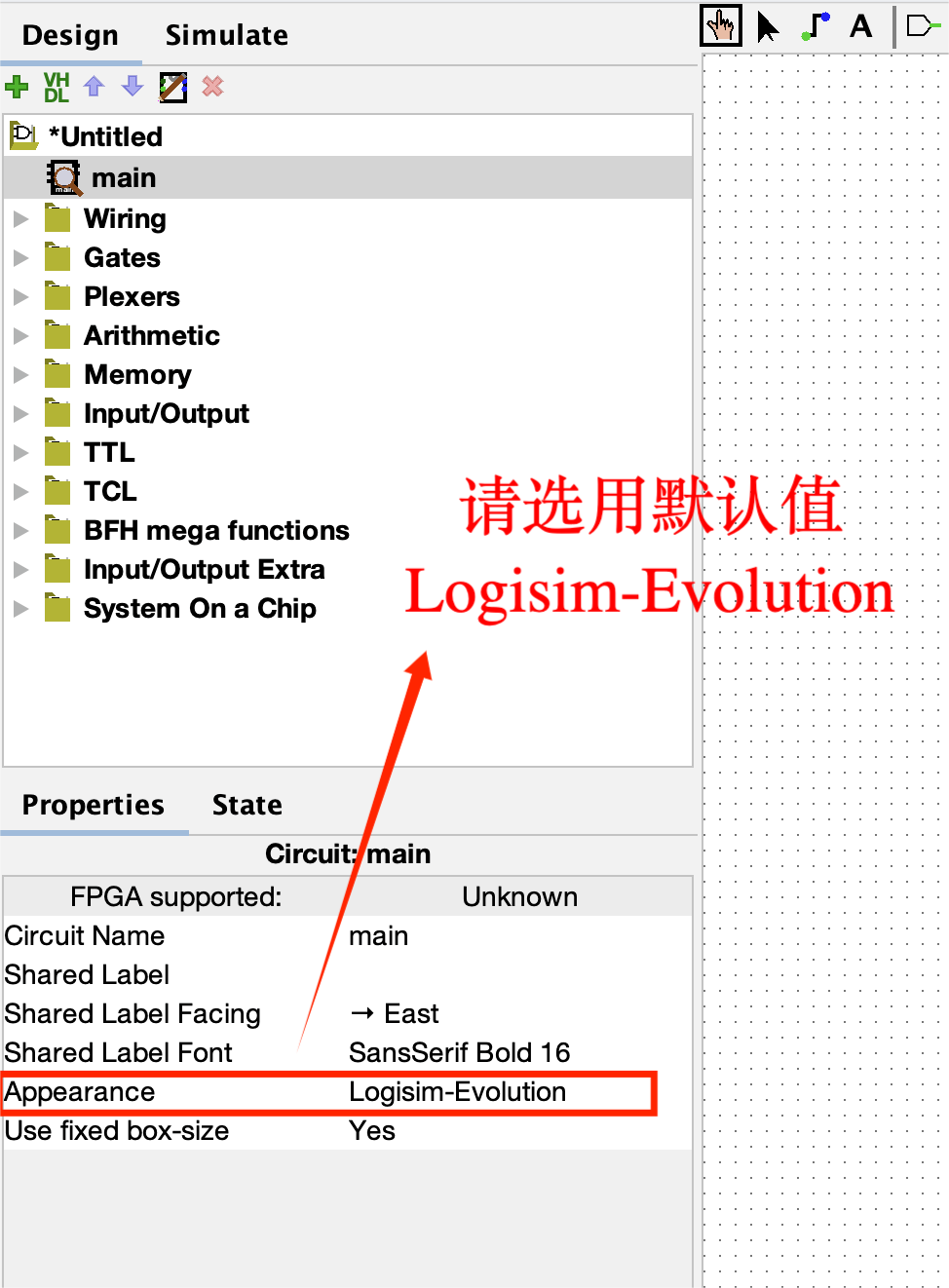
Don't Modify the Appearance of the Circuits!!!
- 随意修改电路的外观可能导致测试不通过!
- 这个问题并不是很常见,因为我们没有任何关于电路外观的要求,一般都是直接使用默认的外观。
3. Homework 1 Guide
关于『红线』、『橙线』、『蓝线』
- 红线说明连接出现致命错误。请不要抱有任何侥幸,仔细检查电路。
- 橙线通常说明位宽不匹配,橙线通常会在两端显示每一端的位宽。
- 位宽是什么?在每一个Tunnel或者Pin原件你都会在properties栏看到Data Bits这一项,这就是位宽。举例:
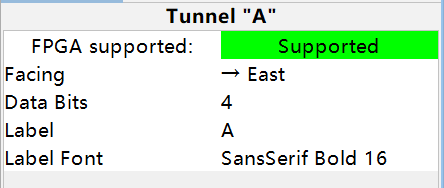
- 数字信号输入“0”和“1”的位宽都是1。
- 数字信号输入“101”和“010”的位宽都是3,“010”本身的十进制值是2,在二进制下为“10”,是两位的,但“010”这个信号的位宽不会因为自身的值而发生改变,仍然是3。
- 位宽是什么?在每一个Tunnel或者Pin原件你都会在properties栏看到Data Bits这一项,这就是位宽。举例:
- 蓝线说明这条线尚未有信号通过,是常见形态,输入信号后即呈现绿色。
3. Homework 1 Guide
元件的规范使用(一)Tunnels
Tunnel的规范使用如下,它会简化导线连接在电路图上的呈现。
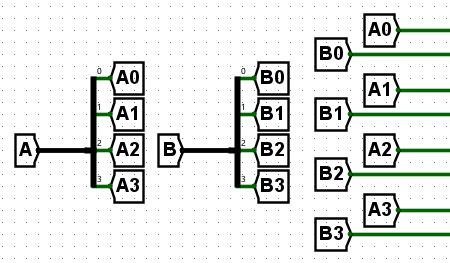
元件的规范使用(二)Pins & Constants
Pin 能够创造一个数字信号输入电路,但是请不要对着一个Tunnel输入两组数字信号!
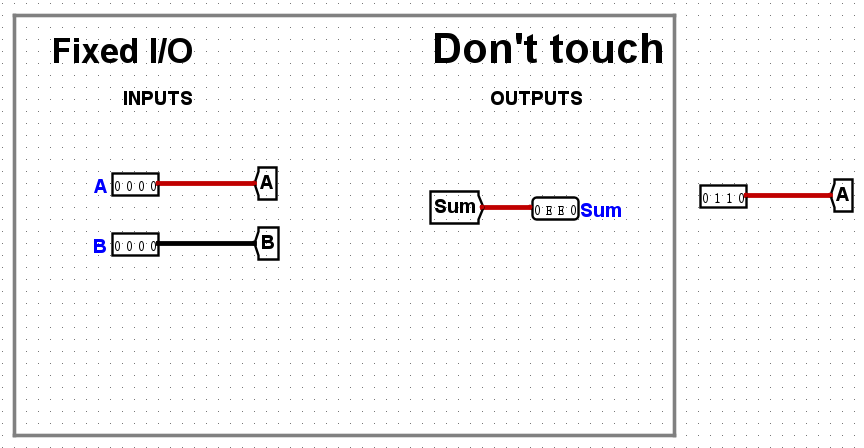
- Constant能够创造一个不会更改的数字信号输入电路(例如“0”、“1”、“010”),它的使用方式和Tunnel和Pin一样。
3. Homework 1 Guide
元件的规范使用(三)Splitter
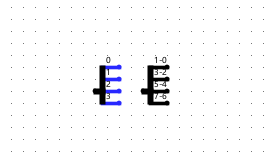
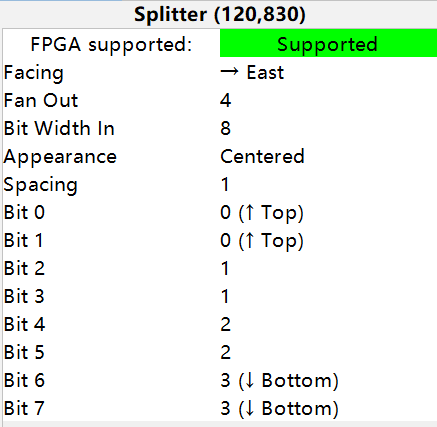
Splitter 能够将一路多位数字信号输入拆分为多路一位(或多位)数字信号输入。下面展示了一个将一路八位信号输入拆分为四路两位信号输出的Splitter:
Bit Width In是输入的数字信号的位宽。Fan Out是输出数字信号的路数,也就是个数。- 最后八行:
- 左侧从上到下分别是输入信号从最低位0到最高位7的每一位。
- 右侧从上到下分别表示这一位在四路输出信号中的哪一路。
例如,输入信号10010101,输出信号从低到高四路为:- 输出第一路(0-1位):10 | 输出第二路(2-3位):10
- 输出第一路(4-5位):10 | 输出第一路(6-7位):01
3. Homework 1 Guide
Exercise 1.1: Half-Adder(半加器)
对于一个 1 Bit 的二进制( 0 or 1 )来说,它的加法被定义为:
- 0 + 0 = 0 | 1 + 0 = 1
- 0 + 1 = 1 | 1 + 1 = (1)0
其中,在 1+1 中出现的 (1) 被称之为“进位”标志。因此,在硬件上,我们定义半加器有两个输入 a 和 b 和两个输出 sum(表示 1 Bit 加法的结果) 和 cout(表示进位),其公式为:
半加器只能执行 1 Bit 的加法运算,这显然不够“给力”。我们需要进一步分析加法的逻辑,来构建更加有用的加法单元:全加器。
3. Homework 1 Guide
Exercise 1.2:全加器
全加器的核心是考虑了进位(被记为 cin)。对于某一位来说,我们除了考虑两个加数的对应位数 a 和 b,还要考虑是否有前一位传来的进位信息。因此,我们的输入就有三个数:a,b,cin。我们需要构建这三个数到输出 sum 和 cout 的逻辑运算。
运行逻辑
cout:a、b、cin之中至少两个为高电平时,输出高电平。此时我们对输入两两取逻辑与,如果a、b、cin之中至少有两个高电平,那么三个逻辑与的输出也至少有一个为高电平,对逻辑与的三个输出取逻辑或即可。sum:a、b、cin之中仅有一个或全部为高电平时,输出高电平。将a、b、cin输入一个三输入异或门即可。(注意!这里的“三输入异或门”有不同的定义方式,请参考 Piazza 上的解答)
3. Homework 1 Guide
Exercise 1.2: 全加器
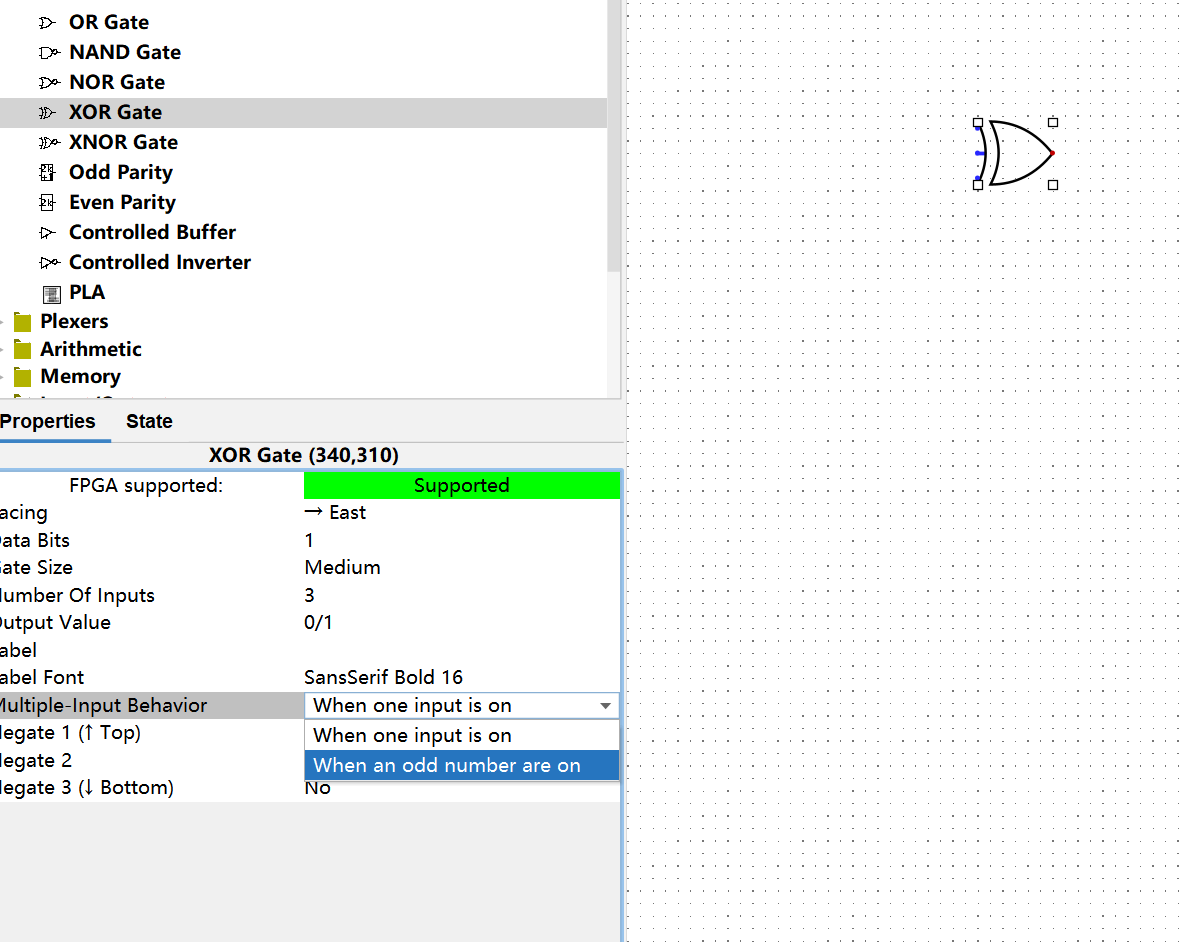
关于“三输入的异或门”的两种定义方式:
- “When One Input is On":只有一个输入为高电平时,输出高电平。
- “Odd Number of Inputs On":奇数个输入为高电平时,输出高电平。
你可以仔细思考一下这两种定义方式的异同,然后想一想,我们的全加器应该使用哪种定义方式。
3. Homework 1 Guide
Exercise 2.1: 4-Bit Full Adder
刚才,我们设计了一位的全加器。这种全加器引入了 Cin 和 Cout 的概念,可以很方便的扩展到多位全加器,从而实现我们常规认知意义上的加法运算。
现在,我们尝试将 1-Bit 的全加器扩展到四位:我们需要四个输入 A、B、C、D,四个输出 Sum 和 Cout。我们需要将四个全加器连接起来,使得每一个全加器的 Cout 都连接到下一个全加器的 Cin 上。
3. Homework 1 Guide
Exercise 2.1: 4-Bit Full Adder
在全加器的实现中,我们忽略可能出现的“多”的一位(称之为“溢出”位),这个值体现为全加器模块 Cout 的值,例如:
0b1111(15) + 0b1111(15) = 0b11110(30)
- 这里我们的全加器输出应该是
(Cout)1 (其他部分)1110 - 我们只需要输出
1110部分即可。
3. Homework 1 Guide
Exercise 2.2: Subtracter
所谓“补码”,是指在二进制数的表示中,用一种特殊的方式表示负数:
- 正数直接由二进制表示。
- 例如:5 被表示为
0101。
- 例如:5 被表示为
- 负数的表示是将对应正数的二进制表示的每一位取反,然后加1。
- 例如:-5 对应的正数是 5,其二进制表示是
0101,取反得到1010,加1得到1011。
- 例如:-5 对应的正数是 5,其二进制表示是
在数字电路中,如果我们使用补码实现数字的表示,则“对一个数取负数”的操作是非常简单的。
3. Homework 1 Guide
Exercise 2.2: Subtracter
使用了 Cin 和 Cout 结构的全加器可以很方便的实现减法:
- 把最低位的 Cin 接到常数 1 上(表示 +1)
- 把输入 B 取反
我们就得到了一个减法器。事实上,这个减法器所计算的结果就是
- 注意,减法器也不需要考虑最高位
Cout的输出。
3. Homework 1 Guide
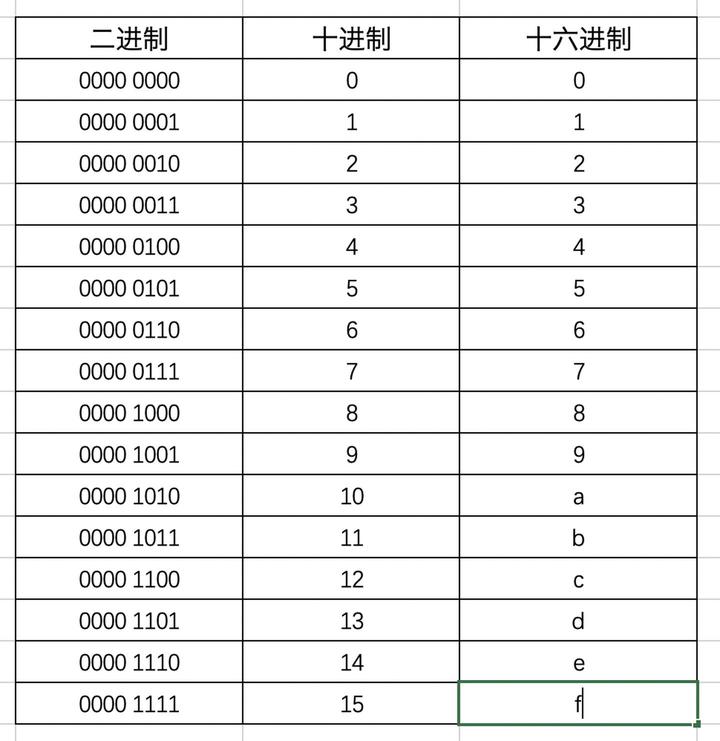
Exercise 3: 七段数码管的解码器
七段 LED 数码管是一种常用的显示元件,常应用于手表、计算器等仪器中,用于显示数值。
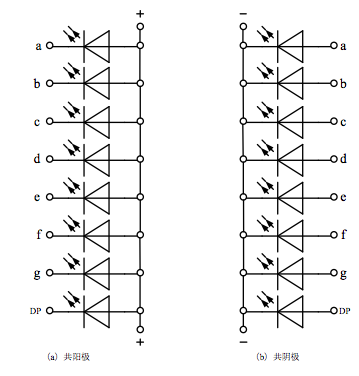
数码管分为共阴极和共阳极两种类型:
- 共阴极就是将七个 LED 的阴极连在一起,让其接低电平。这样给任何一个 LED 的另一端高电平,它便能点亮。
- 而共阳极就是将七个 LED 的阳极连在一起,让其接高电平。这样,给任何一个 LED 的另一端低电平,它就能点亮。
这里的 LED 是共阴极 LED。
3. Homework 1 Guide
Exercise 3: 七段数码管的解码器
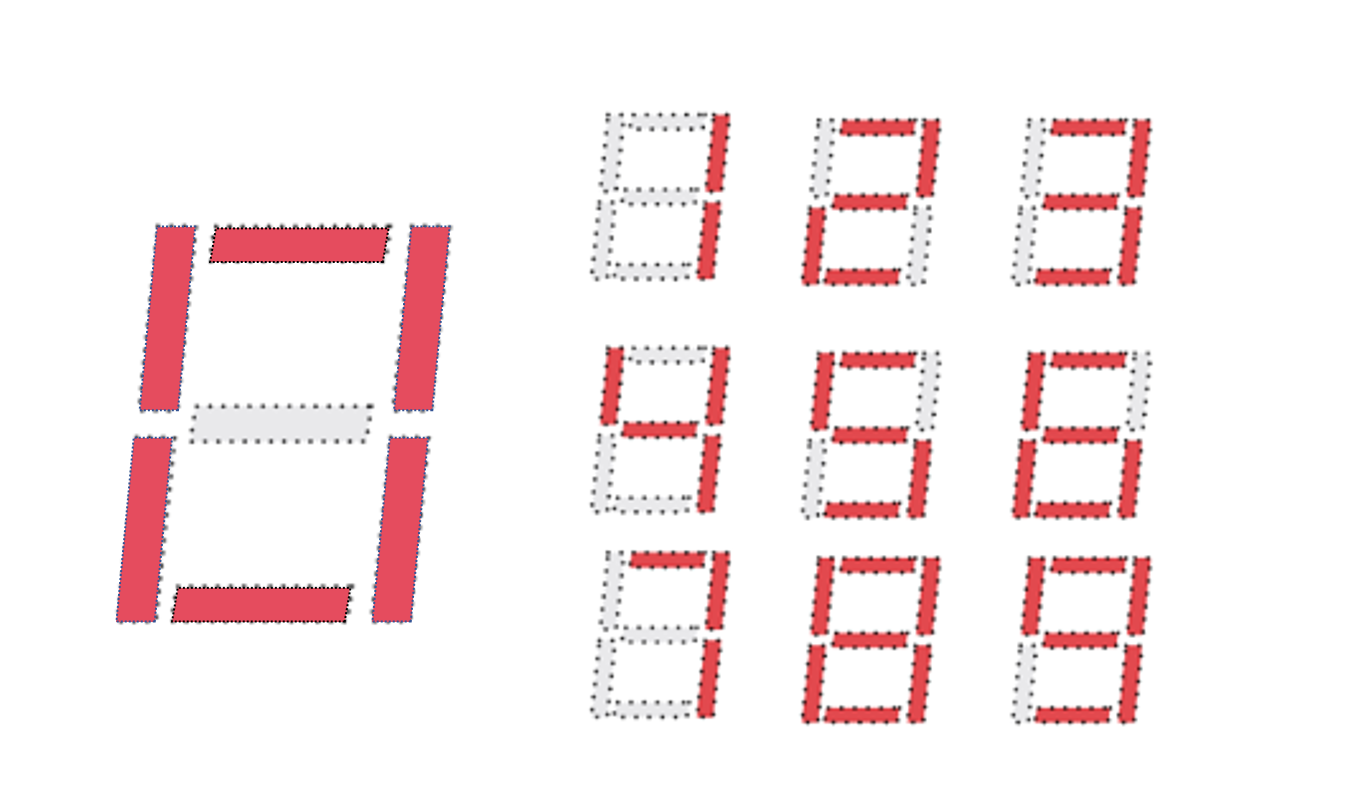
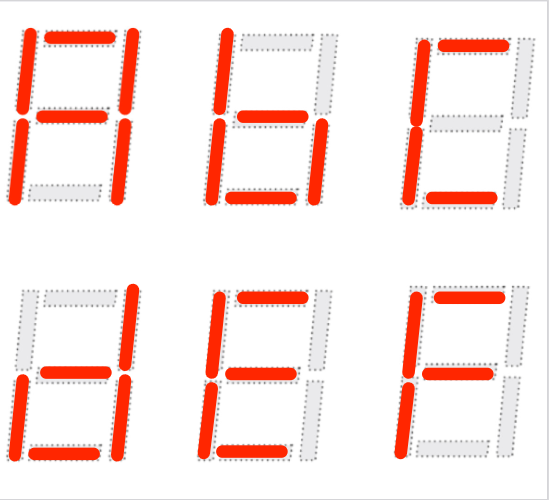
右图为数码管显示的数字 0~9 及十六进制的 a~f 的显示方式。
可以看到,每一个数字或字母都可以用七个二进制位表示,每一个二进制位对应数码管的一个引脚。我们所要做的就是将输入的数字或字母转换为七个二进制位,然后输出到数码管的引脚上。
3. Homework 1 Guide
Exercise 4: 七段数码管的解码器
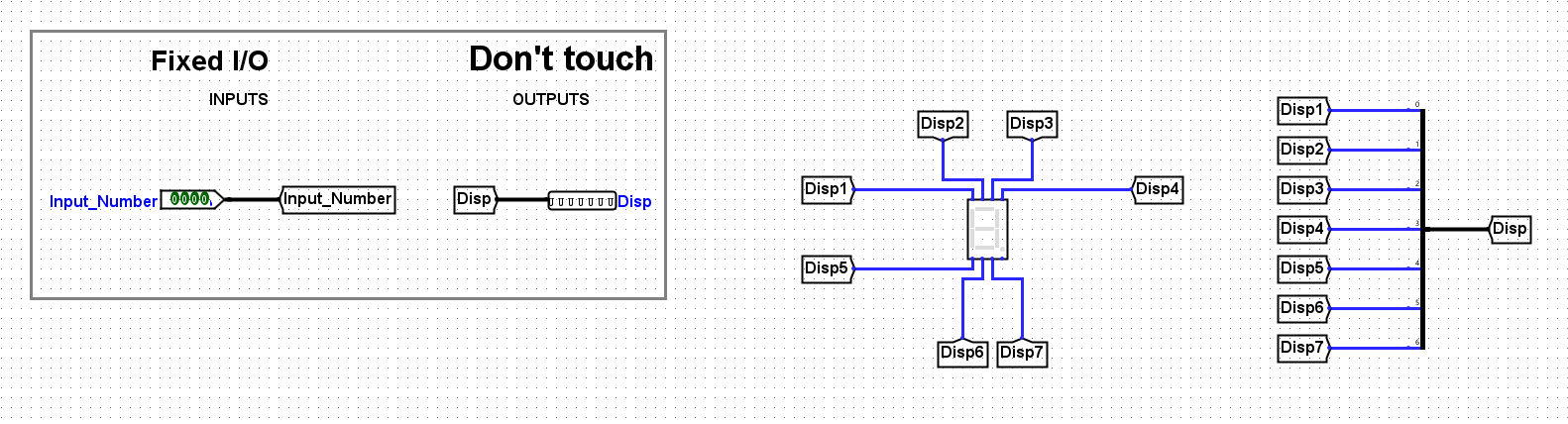
我们将以1号管为例讲解。观察.circ文件:
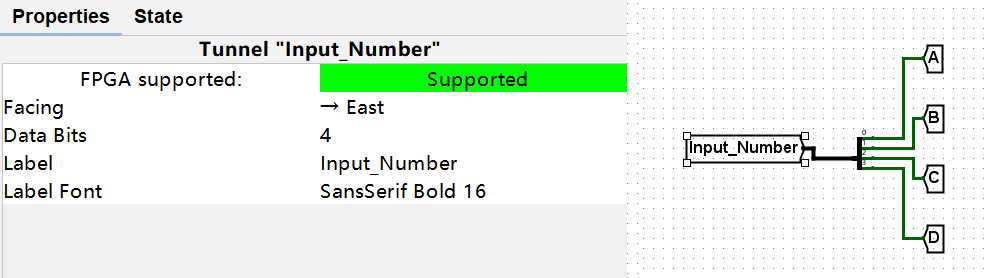
- Input_Number: 是一个四位二进制输入
- Disp: 是一个七位二进制输出
既然只研究1号管,我们只需要关心: 四位输入是如何决定Disp1的高低电平的?
3. Homework 1 Guide
Exercise 4: 七段数码管的解码器
在 4-1 选择器中,我们已经熟悉了两位二进制输入表示一位四进制的想法,这里我们用分线器将输入拆分为独立的四个二进制输入 A、B、C、D。
3. Homework 1 Guide
Exercise 4: 七段数码管的解码器
Exercise 4: 七段数码管的解码器
你的工作流程应该是:。
真值表
- SOP:Sum Of Product
- 卡诺图:用于化简 SOP 逻辑表达式的一种工具
- AOI:And Or Inverter (反相器,用于实现 Not 逻辑) 电路,只有and or not门的电路
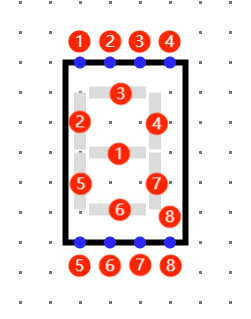
我们将以1号管为例讲解。
3. Homework 1 Guide
Exercise 4: 七段数码管的解码器
- 需要点亮一号管的数是:
2 3 4 5 6 8 9 A B d E F - 因此,我们需要构建的电路只在这些数的时候输出高电平。
- 最简单的方法是:直接构造对应的 SOP 表达式。但这样的工作量非常巨大。
- 因此需要对这个表达式进行化简,这里我们可以使用卡诺图。
- 接下来,按照我们上面给出的 Practice Example 的方法,构建电路即可。