CS182 Final Review

Overview to Superviced Learninng

Statistical Decision Theory

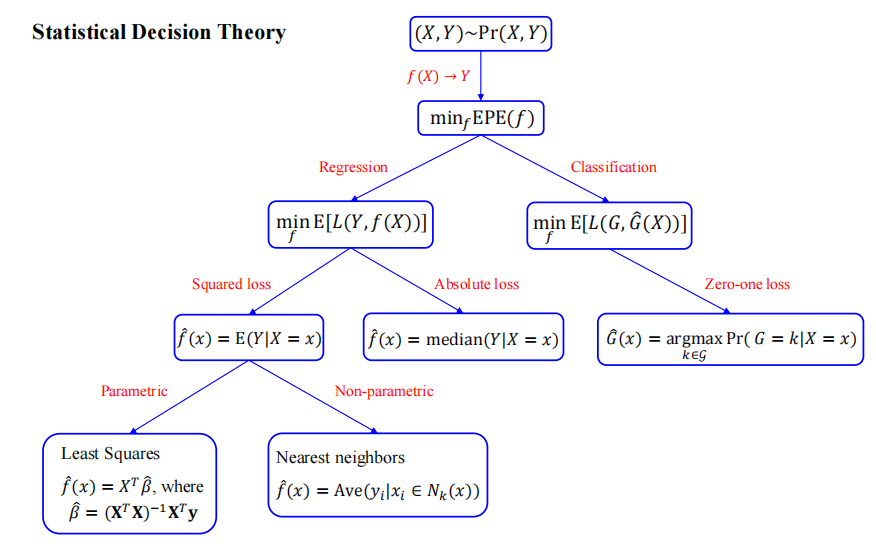
• Squared error loss: $L(Y, f(X)) = (Y-f(X))^2$
• Expected Prediction Error (EPE): $EPE(f) = E(Y-f(X))^2 = \int(Y-f(x))^2Pr(dx, dy)$
  • Noticed that $Pr(dx, dy) = Pr(Y|X)Pr(X)$ , we have $EPE(f) = E_XE_Y([Y-f(x)]^2 | X)$

Local Methods in High Dimensions

Curse of Dimensionality (维度的诅咒)

1. Local neighborhoods become increasingly global, as the number of dimension increases
2. In high dimensions, all samples are close to the edge of the sample
3. Samples sparsely populate the input space

The Bias-Variance Decomposition:

1. Deterministic Case: $\text{MSE}(x_0) = \text{Var}(\hat{y_0})+\text{Bias}^2(\hat{y_0})$

   $\begin{aligned}\text{MSE}(x_0) &= E[f(x_0)-\hat{y}_0]^2\
   &= E[\hat{y}_0 - E(\hat{y}_0)+E(\hat{y}_0)-f(x_0)]^2\
   &= E\big[(\hat{y}_0-E(\hat{y}_0))^2 + 2(\hat{y}_0-E(\hat{y}_0))(E(\hat{y}_0)-f(x_0))+(E(\hat{y}_0)-f(x_0))^2\big]\
   &=E\big[(\hat{y}_0-E(\hat{y}_0))^2\big]+(E(\hat{y}_0)-f(x_0))^2\
   &=\text{Var}(\hat{y}_0)+\text{Bias}^2(\hat{y}_0)
   \end{aligned}$

2. Non-deterministic Case

   $$
   \begin{aligned}\text{EPE}(x_0) &= \text{MSE}(x_0)+\sigma^2\
   &= \text{Var}(\hat{y}_0)+\text{Bias}^2(\hat y_0)+\sigma^2\end{aligned}
   $$

Linear Regression

Simple-Multiple Linear Regression

For $\hat{\mathbf{y}} = \mathbf{X}\beta$, Minimize $\text{RSS}(\beta) = (\mathbf{y}-\mathbf{X}\beta)^T(\mathbf{y}-\mathbf{X}\beta)$

• $\displaystyle\frac{\partial\text{RSS}}{\partial\beta} = -2\mathbf{X}^T(\mathbf{y}-\mathbf{X}\beta) = 0 \Rightarrow \mathbf{X}^T(\mathbf{y}-\mathbf{X}\beta) = 0$

So we have $\hat\beta = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{y}$

Gauss-Markov Theorem

The least squares estimator has the lowest sampling variance within the class of linear unbiased estimators.

最小二乘估计器在线性无偏估计器类中具有最低的抽样方差。

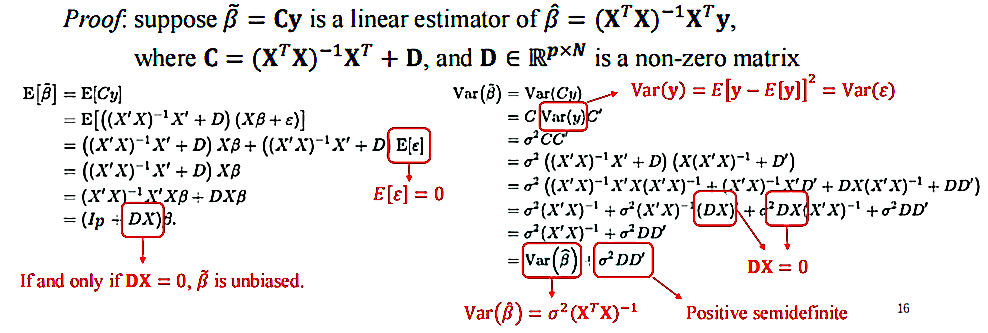
Ridge Regression

对 Regression Coefficients 进行收缩（Shrink）：

$$
\hat{\beta}^{\text{ridge}} = \text{argmin}\beta
\left\lbrace\sum{i=1}^N(y_i-\beta_0-\sum_{j=1}^p x_{ij}\beta_j)^2 + \lambda\sum_{j=1}^p\beta_j^2\right\rbrace
$$

另一个等价的表述是：

$$
\argmin_\beta\sum_{i=1}^N\left(y_i-\beta_0-\sum_{i=1}^px_{ij}\beta_j\right)^2\quad\text{subject to }\sum_{j=1}^p\beta_j\leq t
$$

其中的损失项变为：

$$
⁍
$$

求导令之为 0，得到： $\beta^{\text{ridge}} = (\mathbf X^T\mathbf X + \lambda\mathbf{I}_p)^{-1}\mathbf X^T\mathbf y$

The Lasso

岭回归的 L2-Loss $\displaystyle ||\beta||2 = \sum{j=1}^p|\beta_j|^2$ 变为 L1-Loss $\displaystyle||\beta||1 = \sum{j=1}^p |\beta_j|$

Linear Classification

Linear regression of an indicator matrix

Categorical output variable $𝐺$ with values from $\mathcal G = \lbrace1, … ,𝐾\rbrace$ .

• The zero-one loss $L(k, l) = \begin{cases}1,&k\neq l\0,&k=l\end{cases}$

• EPE with $Pr(G, X)$: $\text{EPE} = E[L(G,\hat G(X))]$

• Pointwise minimize leads to:

  $$
  \hat G(x) = \argmin_{k\in\mathcal G}\sum_{l=1}^KL(K,l)Pr(G=l|X=x) = \argmax_{k\in\mathcal G}Pr(G=k|X=x)
  $$

Basic Idea

Model the posterior $Pr(G=k|X=x)$ based on Bayes Theorem

The Posterior:

$$
Pr(G=k|X=x) = \frac{Pr(X=x|G=k)Pr(G=k)}{Pr(X=x)}=\frac{Pr(X=x|G=k)Pr(G=k)}{\sum_{l=1}^K Pr(X=x|G=l)Pr(G=l)}
$$

其中， $G=k$ 时候 $X$ 的密度为 $f_k(x) = Pr(X=x|G=k)$，而先验有 $\pi_k = Pr(G=k)$

$$
Pr(G=k|X=x)=\frac{f_k(x)\pi_k}{\sum_{l=1}^K f_l(x)\pi_l}
$$

****It produces LDA, QDA (quadratic DA), MDA (mixture DA), kernel DA and naive Bayes, under various assumptions on $f_k(x)$

LDA: Linear Discriminant Analysis

Assumptions in LDA

• Model each class density as Multivariate Gaussian

  $$
  f_k(x)=\frac{1}{(2\pi)^{p/2}|\Sigma_k|^{1/2}}\exp\left(-\frac{1}{2}(x-\mu_k)^T\Sigma_l^{-1}(x-\mu_k)\right)
  $$

• Assume the classes share a common covariance $\Sigma_k = \Sigma, \forall k$

Compare two classes $k$ and $l$

$$
\begin{aligned}\log\frac{Pr(G=k|X=x)}{Pr(G=l|X=x)} &= \log\frac{f_k(x)}{f_l(x)}+\log\frac{\pi_k}{\pi_l}\
&=\log\frac{\pi_k}{\pi_l}-\frac{1}{2}(\mu_k+\mu_l)^T\Sigma^{-1}(\mu_k-\mu_l)+x^T\Sigma^{-1}(\mu_k-\mu_l)\end{aligned}
$$

二次项由于共同的协方差而消失

QDA: Quadratic Discriminant Analysis

Assume that each class has a specific covariance $\Sigma_k$

Discriminant Functions:

$$
\delta_k(x)=-\frac{1}{2}\log|\Sigma_k|-\frac{1}{2}(x-\mu_k)^T\Sigma_k^{-1}(x-\mu_k)+\log\pi_k
$$

Probability and Estimator

MLE: Maximum Likelihood Estimate

Choose $\theta$ that maximizes probability of observed data $\mathcal D$

$$
\hat{\theta} = \argmax_\theta P(\mathcal D|\theta)
$$

MAP: Maximum a Posterior

Choose $\theta$ that is most probable given prior probability and the data

$$
\begin{align}
\hat{\theta} &= \argmax_\theta P(\theta|\mathcal D)\
&= \argmax_\theta \frac{P(\mathcal D|\theta)P(\theta)}{P(\mathcal D)}
\end{align}
$$

Naive Bayes

• Train Naive Bayes:
  • for each value $y_k$
    • estimate $\pi_k \equiv P(Y=y_k)$
    • for each value $x_{ij}$ of each attribute $X_i$
      • estimate $\theta_{ijk}\equiv P(X_i = x_{ij}|Y=y_k)$
• Classify
  • $Y^{\text{new}} \leftarrow \argmax_{y_k}P(Y=y_k)\prod_iP(X_i^{\text{new}}|Y=y_k)$
  • $Y^{\text{new}}\leftarrow \argmax_{y_k} \pi_k\prod_i\theta_{ijk}$

Estimate Parameters

Continuous $X_i$ (Gaussian Naive Bayes)

Assume:

$$
P(X_i=x|Y=y_k)=\frac{1}{\sigma_{ik}\sqrt{2\pi}}\exp\left(\frac{-(x-\mu_{ik})^2}{2\sigma_{ik}^2}\right)
$$

Kernel Method & SVM

The online Learning Model: Perceptron

Algorithm

• Set $t=1$, start with all zero vector $w_1$
• Given example 𝑥, predict positive iff $w_t\cdot x\geq 0$
• On a mistake, update:
  • Mistake on positive, then update $w_{t+1}\leftarrow w_t+x$
  • Mistake on negative, then update $w_{t+1}\leftarrow w_t-x$
• Note: $w_t = a_{i1}x_{i1}+\cdots + a_{ik}x_{ik}$

Geometric Margin

• Definition: The margin of example $𝑥$ w.r.t. a linear sep. $𝑤$ is the distance from $𝑥$ to the plane $w\cdot x=0$
• The margin $\gamma_w$ of a set of examples $𝑆$ w.r.t. a linear separator $𝑤$ is the smallest margin over points $𝑥∈𝑆$.
• The margin $\gamma$ of a examples $S$ is the maximum $\gamma_w$ over all linear seps $w$

Mistake Bound

Theorem: If data linearly separable by margin $\gamma$ and points inside a ball of radius $𝑅$, then Perceptron makes $≤ 𝑅/\gamma^2$ mistakes.

SVMs

Directly optimize for the maximum margin separator:

• Input: $S=\lbrace(x_1,y_1),\dots,(x_m,y_m)\rbrace$
• Maximize $\gamma$ under:
  • $||w||^2 = 1$
  • $\forall i, y_iw\cdot x_i\geq \gamma$

让 $w’ = \frac{w}{\gamma}$，把优化问题转化成凸问题：

• Maximize $||w’||^2$ under $\forall i, y_iw’\cdot x_i\geq 1$
• If data isn’t perfectly linearly separable?
  • Replace “# mistakes” with upper bound called “hinge loss”
  • Minimize $||w||^2+C\sum_i\xi_i$ s.t. $\forall i, y_iw\cdot x_i\geq 1-\xi_i, \xi_i \geq 0$

Lagrangian Dual of SVMs

Kernels

$K(⋅,⋅)$ is a kernel if it can be viewed as a legal definition of inner product:

$$
\exists \phi:X\rightarrow \mathbb R^N,\text{ s.t. }K(x,z)=\phi(x)\cdot\phi(z)
$$

Theorem (Mercer)

K is a kernel if and only if:

• K is symmetric
• For any set of training points $𝑥_1, 𝑥_2, … , 𝑥_𝑚$ and for any $𝑎_1, 𝑎_2, … , 𝑎_𝑚 ∈ \mathbb R$, we have:

$$
\sum_{i,j}a_ia_jK(x_i,x_j)\geq 0\
a^TKa\geq 0
$$

I.e., $K=(K(x_i,x_j))_{i,j = 1,…,n}$ is positive semi-definite

Kernels

• Linear: $K(x,z)=x\cdot z$
• Polynomial: $K(x,z)=(x\cdot z)^2$ or $K(x,z)=(1+x\cdot z)^d$
• Gaussian: $K(x,z)=\exp\left[-\frac{||x-z||^2}{2\sigma^2}\right]$
• Laplace: $K(x,z)=\exp\left[-\frac{||x-z||}{2\sigma^2}\right]$

MLP

反向传播四公式

BP1

If $Y=\sigma(X)$, then:

$$
\frac{\partial L}{\partial X}=\frac{\partial L}{\partial Y}\odot \sigma’(x)
$$

Where $\odot$ means element-wise product

BP2 & 3 & 4

If $Y=W\cdot X+B$

$$
\frac{\partial L}{\partial X}=W^T\cdot \frac{\partial L}{\partial Y}
$$

$$
\frac{\partial L}{\partial B}=\frac{\partial L}{\partial Y}
$$

$$
\frac{\partial L}{\partial W}=\frac{\partial L}{\partial Y}\cdot X^T
$$

推导的核心

考虑： $y_i = w_{i1}x_1+w_{i2}x_2+\cdots+w_{in}x_n + b_i$

$$
\frac{\partial y_i}{\partial w_{ij}}=x_j,\quad \frac{\partial y_i}{\partial x_j}=w_{ij},\quad \frac{\partial y_i}{\partial b_i} = 1
$$

常用损失函数的导数

Softmax

If $X=[x_1,\cdots, x_n], Y=\text{SoftMax}(X)=[y_1,\cdots, y_n]$

Thus $\displaystyle y_i = \frac{e^{x_i}}{\sum_{j=1}^ne^{x_i}}$ and obviously $\displaystyle \sum_{i=1}^n y_i = 1$

Thus we have:

$$
\frac{\partial y_i}{\partial x_j}=\begin{cases}y_i(1-y_i),&i=j\-y_iy_j,&u\neq j\end{cases}
$$

It’s equal to:

$$
\frac{\partial Y}{\partial X}=\text{diag}(Y)-Y^TY
$$

Sigmoid

We have $\sigma(x)=\text{sigmoid}(x)=\frac{1}{1+e^{-x}}$

$$
\sigma’(x)=\sigma(x)(1-\sigma(x))
$$

Softmax with 交叉熵：

$$
L=-\sum_k \hat y_k\log y_k
$$

We have:

$$
\frac{\partial L}{\partial X} = Y-\hat Y
$$

Tanh

We have $\displaystyle\tau(x)=\tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

$$
\tau’(x)=1-\tau^2(x)
$$

Dimension Reduction: PCA

Denoted that $v_1,\dots, v_d$ are the d principal components, $v_i\cdot v_j = \begin{cases}1,&i=j\0,&i\neq j\end{cases}$

Let $X=[x_1,\dots,x_n]$ (Columns are the datapoints)

Maximizes sample variance of projected data

$$
\frac{1}{n}\sum_{i=1}^n(\mathbf v^Tx_i)^2=\mathbf v^T\mathbf X\mathbf X^T\mathbf v\text{ s.t. }\mathbf v^T\mathbf v = 1
$$

Lagrangian: $\argmax_{\mathbf v}\mathbf v^T \mathbf X\mathbf X^T\mathbf v-\lambda \mathbf v^T\mathbf v$

We finally have $(\mathbf X\mathbf X^T -\lambda\mathbf I)\mathbf v=0$, $(\mathbf X \mathbf X^T)\mathbf v = \lambda \mathbf v$

💡 这里的 $\mathbf v^T\mathbf X$ 是投影，再乘上 $\mathbf v$ 就是 在投影上的向量。

• The eigenvalue $\lambda$ denotes the amount of variability captured along that dimension (aka amount of energy along that dimension).
• Zero eigenvalues indicate no variability along those directions $\Rightarrow$ data lies exactly on a linear subspace
• Only keep data projections onto principal components with non-zero eigenvalues, say $v_1, … , v_k$, where $k=\text{rank}(\mathbf X\mathbf X^T)$

Clustering: KMeans

Denotions

• Given a sample $\mathcal X=\lbrace\mathbf x^t\rbrace_{t=1}^N$
• Find $k$ reference vectors $\mathbf m_j$ which best represent the data

Encoding/Decoding

Each data point $\mathbf x^t$ is represented by the index $i$ **of the nearest reference vector $i=\argmin_j||\mathbf x^t-\mathbf m_j||$

We can use labels $\mathbf b^t$ for $\mathbf x^t$ as:

$$
b_i^t=\begin{cases}1&\text{if }i=\argmin_j||\mathbf x^t-\mathbf m_j||\
0&\text{otherwise}\end{cases}
$$

The Total Reconstruction Error:

$$
E(\lbrace\mathbf n_i\rbrace_{i=1}^k|\mathcal X)=\sum_t\sum_ib_i^t||\mathbf x^t-\mathbf m_i||^t
$$

Optimization

$$\argmin_{\lbrace\mathbf{m}i\rbrace{i=1}^k,\lbrace\mathbf{b}^t\rbrace_{t=1}^N}\sum_t\sum_i b_{i}^{t}||\mathbf{x}^t-\mathbf{m}_i||^2\quad$$

However, since $b_i$ also depends on $\mathbf m_i$ , the optimization problem cannot be solved analytically, but iteratively

Algorithm

Gradient Descent

Basic Problem

$$
\argmin_{x\in\mathbb R^n}f(x)
$$

Iteration: $x^{r+1}=x^r-\gamma_r\cdot\nabla f(x^r)$

Convexity

$$
f(\lambda(x)+(1-\lambda)y)\leq \lambda f(x)+(1-\lambda)f(y)\
f(x)\geq f(y)+\nabla f(y)^T(x-y)\
\nabla^2f(x)\geq 0
$$

L-smooth

$$
||\nabla f(x)-\nabla f(y)||\leq L||x-y||
$$

Descemdent Lemma

$$
|f(x)-f(y)-\nabla f(y)^T(x-y)|\leq \frac{L}{2}||x-y||^2
$$

If $f$ twice-differentiable, L-smooth $\Leftrightarrow$ $\nabla^2f(x)\leq LI, \quad\mathbf d^T\nabla^2 f(x)\mathbf d\preceq L||\mathbf d||^2,\forall \mathbf d$

Convergence Analysis

Optimality measure $M(x^r)$

• Convex: $||x^r-x^*||$ or $f(x^r)-f^*$
• Non-convex: $||\nabla f(x^r)||$

Order of convergence $q$ s.t.

$$
\sup\bigg\lbraceq\big| \lim_{r\rightarrow+\infty}\frac{M(x^{r+1})}{M(x^r)^q}<\infty
$$

• $q=1$ : Linear convergence, $q=2$ : quadratic

Rate of Convergence: Given $q$ ,

$$
\lim_{r\rightarrow\infty}\frac{M(r^{r+1})}{M(x^r)^1}=n
$$

• Sublinear: $\text{Rate} = 1$, Superlinear: $\text{Rate} = 0$

Convergence under Convexity

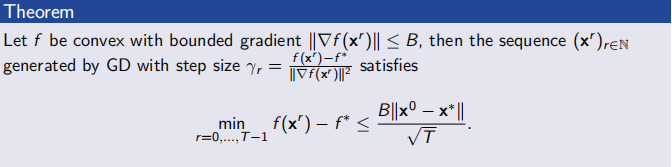
Convergence under Smoothness

Convexity & Smoothness

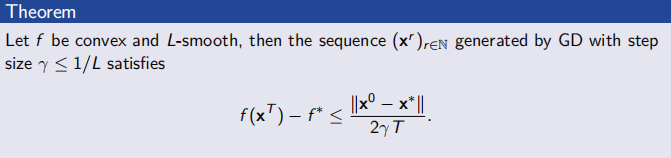
Upper & Lower Bound

$\mu$-Strong Convexity

$$
f(x)\geq f(y)+\nabla f(y)^T(x-y)+\frac{\mu}{2}||x-y||_2^2
$$

L-Smoothness

$$
f(x)\leq f(y)+\nabla f(y)^T(x-y)+\frac{L}{2}||x-y||^2
$$

Implication

$$
\nabla f(x^r)^T(x^r-x^*)\geq f(x^r)-f^*_\frac{\mu}{2}||x^r-x^*||
$$

$$
f(x^{r+1})\leq f(x^r)-\frac{r}{2}||\nabla f(x^r)||^2
$$

Lagrangian

Basics

Original Function

Minimize $f_0(x)$ with optimal $p^*$ subject to $f_i(x)\leq 0, i = 1,…,m$

We have $L(x,\lambda) = f_0(x)+\lambda_1f_1(x)+\cdots+\lambda_mf_m(x)$

Dual Function

$$
⁍
$$

Lower Bound Property: if $\lambda\geq 0$ and $x$ are primal feasible:

$$
g(\lambda)\leq f_0(x)
$$

Dual Problem

Maximize $g(\lambda)$ with optimal $d^*$ subject to $\lambda\geq 0$

We have: $d^\leq p^$ , denoted that $p^*-d^*$ the optimal dual gap.

The Convec Problem have $p^*=d^*$

KKT Optimal Condition

$f_i(x^*)\leq 0$	Primal Feasible
$\lambda_i^*\geq 0$	Dual Feasible
$\lambda_i^f_i(x_i^)=0$	Complementary
$\nabla f_0(x^*)+\Sigma\lambda_i^\nabla f_i(x^)=0$	Stationary

Equality Constraints

Minimize $f_0(x)$ subject to $f_i(x)\leq 0, i = 1,…,m$ and $h_i(x)=0,i = 1,…,p$

We have $L(x,\lambda,v)=f_0(x)+\sum \lambda_i f_i(x)+\sum v_ih_i(x)$

• Dual Function: $g(\lambda, v)=\inf_x(L(x,\lambda,v))$
• Dual Problem: Maximize $g(\lambda, v)$ subject to $\lambda\geq 0$

KKT:

$f_i(x^*)\leq 0, h_i(x^*)=0$	Primal Feasible
$\lambda_i^*\geq 0$	Dual Feasible
$\lambda_i^f_i(x_i^)=0$	Complementary
$\nabla f_0(x^*)+\sum\lambda_i^\nabla f_i(x^)+\sum v_i^\nabla h_i(x^)=0$	Stationary